La transferencia de calor puede verificarse por medio de uno o más de los tres mecanismos de transferencia: conducción, convección o radiación.
Conducción: Por este mecanismo, el calor puede ser conducido a través de sólidos, líquidos y gases. La conducción se verifica mediante la transferencia de energía cinética entre moléculas adyacentes. En un gas las moléculas “más calientes”, que tienen más energía y movimiento, se encargan de impartir energía a moléculas colindantes que están a niveles energéticos más bajos. Este tipo de transferencia siempre está presente, en mayor o menor grado, en sólidos, líquidos y gases en los que existe un gradiente de temperatura. En la conducción la energía también se transfiere por medio de electrones “libres”, un proceso muy importante en los sólidos metálicos. Entre los ejemplos en los que la transferencia se verifica ante todo por conducción, se cuentan la transferencia a través de paredes o intercambiadores de una nevera, el tratamiento térmico en el forjado de acero, la congelación del suelo durante el invierno, etcétera.
La Ley de Fourier de conducción de calor, indica que la taza de conducción de calor en una dirección es proporcional al gradiente de temperatura en esa misma dirección. El calor es conductivo en la dirección de la temperatura decreciente, y el gradiente de temperatura se vuelve negativo cuando la temperatura disminuye con X creciente.
Qcond= -kdT/dX (W)
Donde k: constante de proporcionalidad es la conductividad térmica del material.
La constante de proporcionalidad k es la conductividad térmica del material, la cual es una medida de la capacidad del material para conducir calor.
Ejemplos: Materiales como el cobre y la plata son buenos conductores eléctricos, también lo son para el calor, por lo tanto tienen valores altos de k. El hule, la madera y el poliestireno son malos conductores de calor y por consiguiente, tienen valores bajos de k.
En los sólidos, la conducción de calor se debe a dos efectos:
- Las ondas vibratorias de red inducida por los movimientos vibratorios de las moléculas situadas en una posición relativamente fija en una forma periódica llamada red cristalina.
- La energía transportada a través del flujo libre de electrones en el sólido.
La conducción térmica de un sólido se obtiene al sumar las componentes de la red y electrónicos. La conductividad térmica de los materiales puros se debe sobre todo al componente electrónico, mientras que las de los no metales se debe más que nada al componente de la red cristalina. El componentes de la red cristalina de la conductividad térmica depende en gran medida de la forma que están dispuestas las moléculas.
Conductividad térmica de algunos materiales en condiciones ambiente.
Material Conductividad térmica (W/m.k)
Diamante. 2300
Plata. 429
Cobre. 401
Oro. 317
Aluminio. 237
Hierro 80.2
Mercurio. 8.54
Vidrio. 1.4
Ladrillo. 0.72
Agua. 0.613
Piel humana. 0.37
Madera (roble). 0.17
Helio(g). 0. 152
Hule suave. 0.13
Fibra de vidrio. 0.043
Aire(g). 0.026
Uretano. 0.026
Espuma rígida.
 Pared Plana, Una aplicación inmediata de la ley de Fourier corresponde al caso de la transmisión del calor a través de una pared plana, en la figura. Cuando las superficies de la pared se encuentran a temperaturas diferentes, el calor fluye sólo en dirección perpendicular a las superficies. Si la conductividad térmica es uniforme, la integración de la Ley de Fourier proporciona:
Pared Plana, Una aplicación inmediata de la ley de Fourier corresponde al caso de la transmisión del calor a través de una pared plana, en la figura. Cuando las superficies de la pared se encuentran a temperaturas diferentes, el calor fluye sólo en dirección perpendicular a las superficies. Si la conductividad térmica es uniforme, la integración de la Ley de Fourier proporciona:
En la que L es el espesor de la pared, T1 es la temperatura de la superficie de la izquierda x=0 y T2, es la temperatura de la superficie de la derecha x=L.
Paredes Planas en Serie, Si el calor se propaga a través de varias paredes en buen contacto térmico, capas múltiples, el análisis del flujo de calor en estado estacionario a través de todas las secciones tiene que ser el mismo. Sin embargo y tal como se indica en la figura en un sistema de tres capas, los gradientes de temperatura en éstas son distintos. El calor transmitido se puede expresar para cada sección y como es el mismo para todas las secciones, se puede poner:
Si se considera un conjunto de n capas en perfecto contacto térmico el flujo de calor es:
Paredes en Paralelo, Las ecuaciones anteriores se pueden utilizar en la resolución de problemas más complejos, en los que la conducción tiene lugar en paredes dispuestas en paralelo.
La figura muestra un bloque formado por dos materiales de áreas A1 y A2 en paralelo. En este caso hay que tener en cuenta que para una determinada diferencia de temperaturas a través del bloque, cada capa del conjunto se puede analizar por separado, teniendo presentes las condiciones impuestas para el flujo unidimensional a través de cada una de las dos secciones. Si la diferencia de temperaturas entre los materiales en contacto es pequeña, el flujo de calor paralelo a las capas dominará sobre cualquier otro flujo normal a éstas, por lo que el problema se puede tratar como unidireccional sin pérdida importante de exactitud. Como el calor fluye a través de los dos materiales según trayectorias separadas, el flujo total de calor Qk será la suma de los dos flujos:
en la que el área total de transmisión del calor es la suma de las dos áreas individuales y la inversa de la resistencia total es igual a la suma de las inversas de todas las resistencias individuales.
Paredes compuestas, Una aplicación más compleja del enfoque del circuito térmico sería la indicada en la figura, en la cual el calor se transfiere a través de una estructura formada por una resistencia térmica en serie, otra en paralelo y una tercera en serie.
Para este sistema, el flujo térmico por unidad de superficie es:
en la que n es el número de capas en serie, Ri es la resistencia térmica de la capa i, y ΔTglobal es la diferencia de temperaturas entre las dos superficies exteriores. El análisis del circuito precedente supone flujo unidimensional. Si las resistencias RB y Rc son muy diferentes, los efectos bidimensionales pueden ser importantes.
Sistemas radiales, Los sistemas cilíndricos y esféricos a menudo experimentan gradientes de temperatura sólo en la dirección radial, y por consiguiente se tratan como unidireccionales. Además bajo condiciones de estado estacionario, sin generación de calor estos sistemas se pueden analizar usando la expresión de la Ley de Fourier en las coordenadas adecuadas.
Escribiendo la ecuación anterior en término de integrales con las condiciones de frontera,
T(r1)=Ts,1 y T(r2)=Ts,2. Obtenemos:
Si considerando k=constante y resolvemos, nos queda:
También es posible obtener la distribución de temperaturas en la dirección radial en el cilindro, esto es:
En el caso de la pared cilíndrica, la distribución de temperaturas ya no es lineal, sino logarítmica.
De este resultado, es evidente que la resistencia térmica para la conducción radial es de la
forma
- Paredes esféricas:Considere la esfera hueca de la figura. Para el estado estacionario y condiciones unidimensionales, Qr es constante y la forma apropiada para la ley de Fourier es:
donde Ar=4πr^2 es el área normal a la dirección de transferencia de calor, luego la ecuación anterior se puede expresar en forma integral como:
1. Gases. El mecanismo de conducción térmica de los gases es bastante simple. Las moléculas poseen un movimiento continuo y desordenado y chocan entre sí intercambiando energía y momento lineal. Si una molécula se desplaza de una región de temperatura elevada a otra de temperatura inferior, transporta energía cinética a esa región y la cede al chocar con moléculas de baja energía. Puesto que las moléculas se mueven con más rapidez cuanto menor es su tamaño, los gases como el hidrógeno tienen conductividades térmicas más elevadas. La conductividad térmica aumenta aproximadamente según la raíz cuadrada de la temperatura absoluta y es independiente de la presión por lo menos hasta algunas atmósferas. Sin embargo, a presión muy baja (vacío) la conductividad térmica tiende a cero.
2. Líquidos. El mecanismo físico de conducción de energía en los líquidos es bastante similar al de los gases, ya que las moléculas de energía más alta chocan con las de energía menor. Sin embargo, las moléculas de los líquidos están mucho más juntas entre sí y los campos de fuerza moleculares ejercen un efecto considerable sobre el intercambio de energía. Puesto que no existe una teoría molecular adecuada para los líquidos, la mayoría de las correlaciones para predecir sus conductividades son de tipo empírico. La conductividad térmica de los líquidos varía de manera moderada con la temperatura, variación que casi siempre puede expresarse con una función lineal, k=a+bT donde a y b son constantes empíricas. Las conductividades térmicas de los líquidos son esencialmente independientes de la presión. El agua tiene una conductividad térmica elevada en comparación con los líquidos orgánicos como el benceno, la conductividad térmica de la mayoría de los alimentos sin congelar, como la leche descremada, o el puré de manzana que contiene grandes cantidades de agua, tienen conductividades térmicas cercanas a la del agua pura.
3. Sólidos. Las conductividades térmicas de los sólidos homogéneos son muy variables. Los sólidos metálicos como el cobre y el aluminio tienen valores muy elevados, mientras que algunos materiales aislantes no metálicos, del tipo de la lana mineral y el corcho, tienen conductividades muy bajas. La conducción de calor o energía a través de los sólidos se verifica mediante dos mecanismos. En el primero, que se aplica principalmente a los sólidos metálicos, el calor, al igual que la electricidad, es conducido por los electrones libres que se mueven en la red estructural del metal. En el segundo, que existe en todos los sólidos, el calor es conducido por la transmisión de energía vibracional entre átomos
Formulario de conducción
Ejercicio 1
Ejercicio 2
Ejercicio 3
Ejercicio 4
Ejercicio 5
Ejercicio 6
Ejercicio 7}
ejercios
extra1
extra2
extra3
extra4
- Formulario:
Formulario de conducción
- Ejercicios de conducción:
Ejercicio 1
Ejercicio 2
Ejercicio 3
Ejercicio 4
Ejercicio 5
Ejercicio 6
Ejercicio 7}
ejercios
extra1
extra2
extra3
extra4
( Yurus A. Cengel. Termodinámica Sexta edición. Editorial McGraw-Hil,inc. 2008)
(C. J. Geankopolis. Procesos de transporte y operaciones unitarias. Tercera edicion. Editorial: COMPAÑÍA EDITORIAL CONTINENTAL, S.A. 1998)

















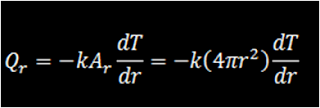



Muy buena información era lo que estaba buscando fácil de entender y de estudiar.
ResponderEliminarExcelente información, me gusto la forma en que explicaron la teoria y los ejercicios ����
ResponderEliminarNajat Mahmoud sección 02
excelente contenido, muy útil y bastante explicito!!
ResponderEliminarExcelente material instructivo. Buen desarrollo del tema. Una buena cantidad de ejercicios para la practica de los mismos.
ResponderEliminarBuena información,los ejercicios me ayudaron mucho
ResponderEliminarDorianney Gómez sección 2
muy bien redactada y explicada la teoría, buen material para la practica. Guillermo mMyorga sección 02
ResponderEliminarBuena información, pero deberían colocar un formulario como tal, me parece algo engorroso tener que estar buscando en todo el contenido cuando se puede tener algo más directo.
ResponderEliminarFrancisco Albornett, sección 04
Gracias. Estamos trabajando en eso, pronto estará el formulario incluido.
EliminarExcelente información y muy buenos ejercicios
ResponderEliminarGracias por la info, chicos. Me gusta que usaron imágenes para la observación de los términos de las formulas, ademas la tabla de conductividad de materiales es muy útil!
ResponderEliminarMariangel Durant
Seccion 02
Excelente información, muy entendible y coherente. De verdad me dejo buenos conocimientos. Me gustaron mucho los ejercicios presentados. Buena esquematización y dinámica en cuanto al uso de imágenes y la tabla de conductividad.
ResponderEliminarI LOVE IT!
ResponderEliminarFascinating!!😉💖👍
ResponderEliminarEsta muy buena la información, me parece muy completa
ResponderEliminar